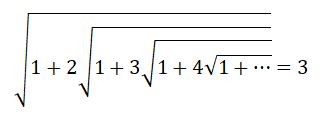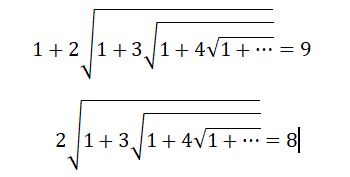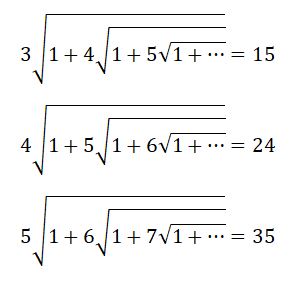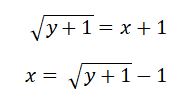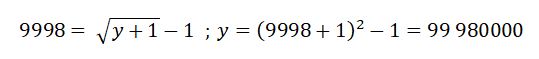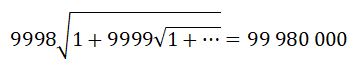Немного математики. Просто о сложном

Возможно, многие из вас слышали про одного из величайших математиков Сриниваса Рамануджана как минимум из фильма «Человек, который познал бесконечность», основанного на реальных событиях. Уникальность этого человека в том, что он, не имея специального математического образования, достиг невероятных результатов в области теории чисел. Многие из его гипотез до сих пор не доказаны, но поражают своей математической красотой. На странице в Википедии мне приглянулась одна из его формул:

Красиво, не правда ли? Никаких сложных математических функций, только бесконечный ряд корней. Но верно ли это равенство? Попробуем доказать?
Легких путей я, конечно, искать не буду, потому предложу необычное решение, которое позволит сократить тонну бумаги. Поэтому давайте посчитаем, что данное выражение верно и тогда подкоренное выражение должно быть равно:

И далее по аналогии:

Уже заметили закономерность? Числовой ряд 8, 15, 24, 35, 48, 63… соответствует закономерности (n^2 – 1) и является бесконечным рядом при всех целочисленных значениях n є [ 3 ; ∞ ) а, значит, что исходное выражение верно. Вот так все просто оказалось!
Тогда, чтобы не заканчивать так быстро, попробуем рассчитать, чему будет равен 9998-ый по порядку корень?
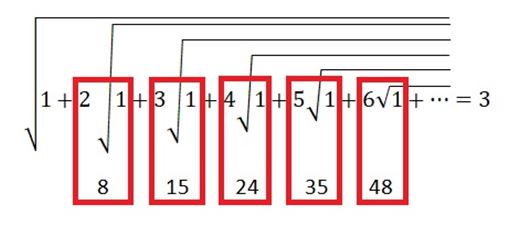
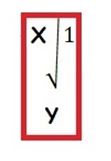
Для этого взглянем на исходное выражение под другим углом и запишем значения коренных множеств непосредственно под ними:

И представим их в общем виде:

Сразу же видна закономерность:

Где x – и есть искомая величина, являющаяся количеством корней. Теперь мы легко вычисляем 9998-ой корень:

То есть:

Вот на этом, я полагаю, можно закончитьобзор этой малой грани теории чисел. Если найдете еще какие-либо закономерности, пишите! Буду рад обсудить.