Давайте попробуем сделать невозможное - научимся контролировать гравитацию!

Универсальность гравитации предполагает, что ее возникновение следует понимать из общих принципов как кооперативный квантовый феномен, так утверждают теоретики.
У нас есть определенное преимущество перед другими исследователями, потому что мы можем рассмотреть возникающую гравитацию с помощью устройства - необычного гироскопа, в котором кооперативное квантовое явление, как оказалось, неоднократно экспериментально подтверждено на ускорителях элементарных частиц.

В наше время в известных работах было продемонстрировано существование глубокой связи между гравитацией и энтропией [1, 2, 3]. В последнее время такие фундаментальные идеи, как Голографический принцип [4, 5] и энтропийная гравитация Э. Верлинде [6], также известная как эмерджентная гравитация, представляют собой теорию современной физики, которая описывает гравитацию как энтропийную силу.

Сегодня Голографический принцип - это сотни теоретических работ известных физиков мирового уровня: Г. т' Хофта, Л. Сусскинда, Я. Д. Бекенштейна, Э. Верлинде, Дж. М. Мальдасена, Р. Буссо .... Уже есть экспериментальные исследования, подтверждающие работу голографического принципа [7], [8]. С 1997 года было опубликовано более 10000 работ в поддержку этой идеи.

MGEF

Для экспериментальной проверки Голографического принципа существует проект MGEF (Модульный генератор энтропийных сил) на основе необычного гироскопа. Если Голографический принцип работает, то можно искусственно создавать гравитационные силы дальнего действия, и это позволит нам управлять гравитацией и иметь множество захватывающих приложений, не нарушая фундаментальных законов физики.

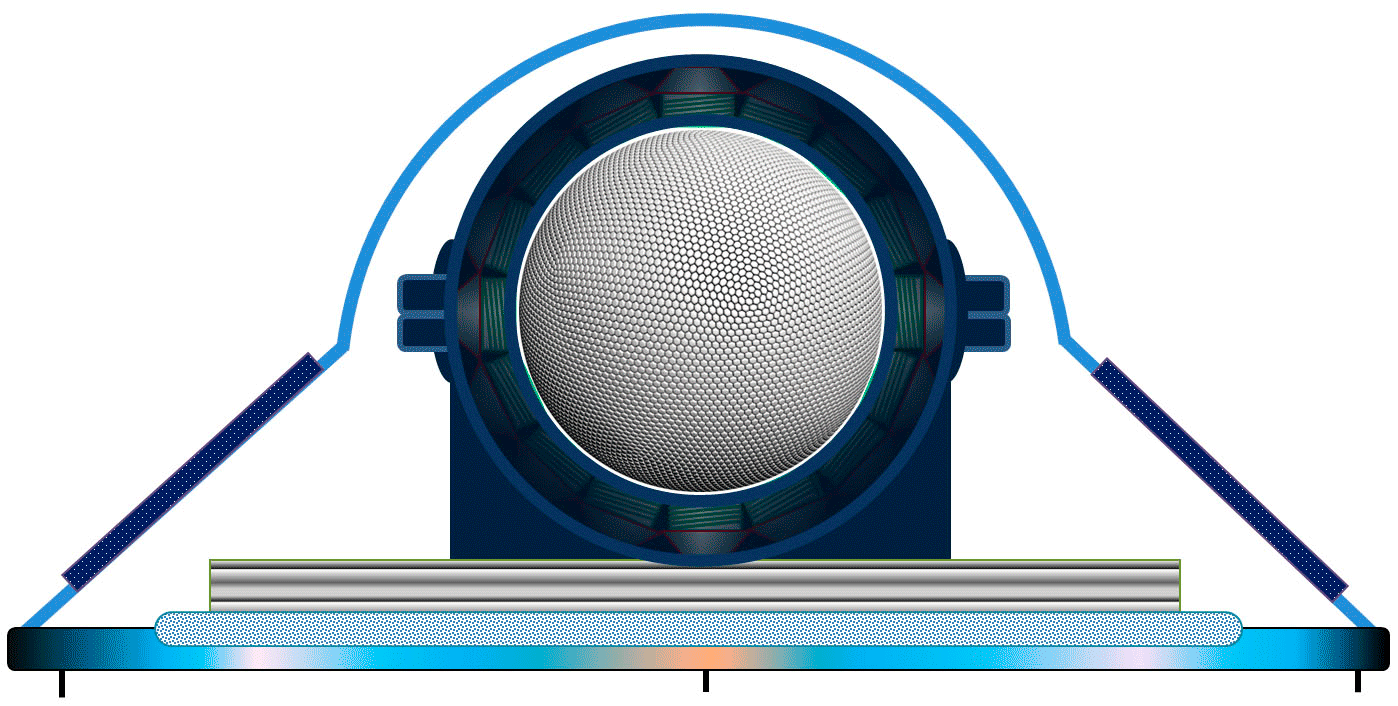
Что это такое необычный гироскоп?

На самом деле это небольшое электромеханическое устройство, которое может занимать десятую часть вашего стола. Сферический ротор необычного гироскопа имеет магниты и вращается в вакууме внутри сферического статора с соленоидами под управлением компьютера (имеются датчики и драйверы для создания вынужденных колебаний ротора). Название "необычный гироскоп" оправдано тем фактом, что его ротор производит полные вынужденные колебания вокруг трех фиксированных осей за цикл. Здесь подавляющее большинство экспертов будут против. Согласно теореме Эйлера о вращении - одновременное вращение по нескольким стационарным осям одновременно невозможно. Тем не менее, я прошу внимания, для полного оборота физического тела (или ротора) вокруг трех фиксированных декартовых осей за цикл - возможно. «Цикл» это ключевое слово. В научной литературе нет описания таких колебаний. Можно использовать одно простое параметрическое уравнение углового смещения точки на роторе по законам гармонических колебаний. Уравнение настолько простое, что непозволяет сделать ошибку.

(Θх = Сosθ
(Θy = Sinθ
(Θz = -Sinθ,

где θx, θy, θz последовательное угловое смещение любой предварительно выбранной точки на экваторе и двух меридианах вокруг вокруг соответствующих осей: где параметры: θ = πt и -1 ≤ t ≤ 1; θ - геометрический угол, измеренный произвольным и предварительно выбранным направлением угловых поворотов. Уравнение задано параметрически, и оно применимо для любого радиуса ротора. Мы можем задать максимальную точность угловых перемещений, если Δt → 0.
Как только гироскоп нового типа - необычный гироскоп был изобретен и испытан на симуляторе, возник вопрос: какими новыми свойствами он может обладать?
Первое, что бросается в глаза, глядя на очень простое уравнение движения ротора, - это то, что колебания ротора когерентны. Поскольку разность фаз трёх искусственно созданных колебаний является постоянной - колебания каждой точки и, соответсвенно, элементов массы ротора - когерентны. Кроме того, используя симулятор, мы можем наблюдать фиксированную интерференционную картину от ускорений (α), связанных с фиксированными декартовыми координатами. Мы можем видеть шесть групп диаметрально расположенных вращательных ускорений за цикл. Если рассчитать все возможные направления таких когерентных колебаний ротора, то их число будет ровно 60 (64 если учесть 4 специфических направления).

Принцип эквивалентности

Принцип эквивалентности говорит нам, что мы не можем различить инерционную и гравитационную массу с помощью эксперимента. Эйнштейн изобрел эксперимент с лифтом. Лифт бесконечно удален от гравитирующих тел и движется с ускорением. Тогда все тела в лифте будут находиться под силой инерции и оказывать давление на поверхность основания лифта. То есть тела будут иметь вес. Если лифт не движется, а висит над гравитирующей массой в однородном поле, все тела также будут оказывать давление на поверхность основания лифта. Таким образом, невозможно различить эти две силы в лифте. Поэтому все механические явления будут происходить одинаково в обоих лифтах. Эйнштейн распространил это утверждение на все массы физических тел во вселенной. Если мы ищем способ управления гравитацией, а аксиома Эйнштейна позволяет нам не проводить различий между силами инерции и гравитации, мы должны воспользоваться этим и учитывать тот факт, что существуют силы инерции, которые зависят от скорости. Например, это сила Кориолиса. Сила Кориолиса отклоняет тело от прямолинейного движения, если эти тела находятся во вращающейся неинерциальной системе отсчета.

Новый тип гироскопа имеет когерентные колебания ротора

Необычный гироскоп представляет собой принципиально новый тип гироскопа, который отличается от любых силовых гироскопов не только отсутствием механических осей и отсутствием газовой подушки, но также когерентными колебаниями сферического ротора в вакуумной полости статора. В то время как ротор обычного гироскопа совершает полный оборот вокруг одной оси за один цикл колебаний, ротор необычного гироскопа вынужден быстро вращаться вокруг трех осей (Ox, Oy, Oz). В этом его концептуальное отличие от любого гироскопа, и эта особенность отражена автором этого текста в формуле соответствующей патентной заявки. Левитация ротора в статоре достигается путем его подвешивания в активной электромагнитной подвеске. Как правило, в трехосных гироскопах используется кардан, который позволяет свободно вращать ротор относительно трех осей, и это делает их сродни необычному гироскопу. Принудительные и полные колебания ротора необычного гироскопа вокруг трех осей за цикл - это его принципиальное отличие от обычного гироскопа.

Таким образом, за цикл когерентных колебаний ротор необычного гироскопа совершает полный оборот вокруг одной фиксированной точки - это геометрический центр, центр масс и центр ускорений и вокруг трех осей декартовых координат.

Например:
Нам дана точность Δt = 1/360. Это означает, что мы начали делать угловые смещения любой точки на поверхности вращения ротора примерно на один градус, например, по закону (Cosθ) вокруг неподвижной оси x в постоянном минимальном интервале времени. В следующий равный и минимальный интервал времени мы можем производить угловые смещения вокруг оси y, но уже по закону (Sinθ) и, соответственно, z (- Sinθ). Но поскольку до конца цикла для каждой оси осталось около 359 градусов, мы продолжим работу такими триадами, которые в конечном итоге завершатся одновременно для всех функций, поскольку разность фаз постоянна. Мы получили цикл когерентных колебаний. Нам пока не нужно знать, как ведут себя точки ротора, каковы их траектории. Функции чередуются, и существует шесть групп направленных (мгновенных) ускорений вращения, связанных с фиксированными декартовыми координатами. В пространстве и во время цикла они занимают постоянные позиции. Получены когерентные колебания элементов массы в вакууме и силы Кориолиса.

Сила Кориолиса

Наша цель - получить максимальную величину ускорений элементов массы и величину силы Кориолиса, действующую на элементы массы ротора. Величина сил Кориолиса зависит от угловой скорости ротора. Можно предположить, что суперпозиция сил Кориолиса, полученных таким образом, эквивалентна фиктивному «гравитационному» полю, действующему на каждый элемент массы ротора. Поскольку силы Кориолиса в замкнутой системе равны друг другу и ортогональны, их результирующая всегда будет равна нулю, а центр масс ротора остается неподвижным. Мы можем увеличить эти силы, увеличив скорость вращения ротора.
Но очень важно понимать, что мы можем искусственно (управляя движением ротора посредством программы) производить рывок и одновременно смещать любые четыре из шести интерференционные картины или, другими словами смещать все точки (все элементы массы), например, вокруг двух из трех фиксированных декартовых координат искусственно на короткое время, создавая декогеренцию. И да, мы можем сделать это в конце цикла. В то же время мы не нарушаем Третий Закон Ньютона до тех пор, пока не утверждаем, что центр масс ротора должен изменить свое положение в пространстве в такой замкнутой системе.

Другое дело, если работает Голографический Принцип, что косвенно подтверждается в экспериментах. Это позволяет нам расширить размер замкнутой системы до ее максимального размера, голографического экрана Вселенной. И это вселяет надежду получить нескомпенсированную действующую на расстоянии гравитационную силу, приложенную к центру масс ротора необычного гироскопа.

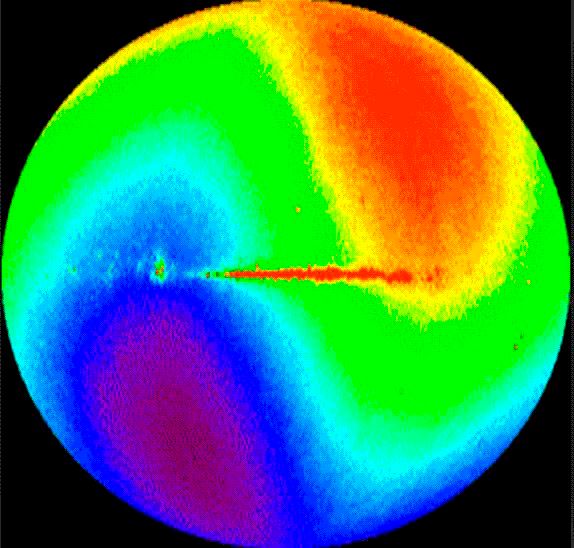
Разница температуры в разных направлениях

Соответствующим по масштабам Голографическому принципу было открытие анизотропии Вселенной в 1992 году (анизотропия космического микроволнового фона - CMB), это разность температур в разных направлениях на небе [9]. Экспериментально подтвержденная анизотропия CMB вместе с открытием когерентных акустических волн в ранней Вселенной имеет большое значение не только для космологии, но и для всего естествознания в целом. Можно сказать, что крупномасштабные трехмерные звуковые когерентные колебания действуют до периода рекомбинации и заканчиваются через 379 000 лет после появления Вселенной, но не исчезают полностью и регистрируют большой масштаб глобального градиента температуры на голографическом экране (согласно Голографическому Принципу проекция всех явлений на голографический экран происходит без потери информации). Чтобы исследовать термодинамику на голографическом экране, мы должны учитывать влияние ее глобальной анизотропии - температуры на динамику проекций. Голографический принцип может раскрыть новый голографический механизм для генерации масс частиц и для всех известных сил и взаимодействий как энтропийной силы.

Контроль гравитации

Примерно половина глобальных градиентов температуры на голографическом экране Вселенной отличаются друг от друга, поэтому две из четырех групп градиентов энтропии (половина из них) обусловлены движением элементов масс ротора (при рывке), проекции испытывают разное взаимодействие с этими областями. Крупномасштабное нарушение симметрии на голографическом экране и результат ускорения элементов массы во время искусственного рвыка приводят к направленной энтропийной силе, которая прикладывается к геометрическому центру (для сферического ротора это центр масс, который совпадает с его геометрический центром).
Мы можем исследовать работу устойства - необычного гироскопа, в котором гравитация возникает вследствие энтропии.
Согласно голографическому принципу, изменение этой энтропии на поверхности голографического экрана, когда материя движеться (вращается и производит ускорения), приводит к энтропийной силе, которая принимает облик гравитации.

Fg = ΔTΔS,

где Fg - гравитационная сила, ΔT - градиент температуры на гравитационном горизонте, ΔS - градиент энтропии, возникающий в результате рывка и / или смещения вещества происходящих в трехмерном пространстве

ΔS ∼ α.

После преобразований мы приходим ко Второму Закону Ньютона [6], и это означает, что гравитацией можно управлять без экзотических масс и энергий. Таким образом, интегральный гравитационный эффект определяется множеством энтропийных сил, как результат взаимодействий проекций ускорений с крупномасштабной (глобальной) дипольной анизотропией, представленной температурой на голографическом экране Вселенной.

Гравитация - это термодинамическое явление. Серия генерируемых управляемых и направленных сил гравитации позволяет нам осуществлять смещение всей конструкции необычного гироскопа в пространстве, в любом выбранном направлении и нереактивным способом. Это означает, что для одной точки - центра и для всех точек, то есть центра масс ротора необычного гироскопа, гравитация, например, гравитация Земли, может быть полностью скомпенсирована и / или преодолена.
Сегодня многочисленные эксперименты с быстрым (7000 об / мин) вращением массы в вакууме демонстрируют дальнодействующие силы в 2,5 Н. Идея, что гравитационная сила может рассматриваться как энтропийная сила, рассматривается в эксперименте [10].

Выводы

Если учесть все возможные направления когерентных колебаний ротора необычного гироскопа, то их количество будет ровно 60 (64 если учесть четыре специфических направления). Это число соответствует количеству элементарных частиц Стандартной модели. И действительно, после загрузки в сертифицированном симуляторе, чрезвычайно простой формулы, описывающей динамику ротора необычного гироскопа, на экране компьютера в изометрии можно наблюдать появление сферического экрана, а также динамику и свойства проекций элементарные частицы. Четыре специфических направления, повидимому, отвечают числу безмассовых или почти безмассовых частиц).

Голографический Принцип заключает, что: гравитация объясняется как энтропийная сила. Принцип эквивалентности приводит нас к выводу, что именно этот закон инерции является источником энтропии. Это термодинамика на экране, возникающая в результате статистического поведения микроскопических степеней свободы, связанных с глобальной анизотропией температуры и локализованных на голографическом экране Вселенной. Таким образом, сила тяжести и её дальнодействие не постулируются, а происходят из голографического сценария.

В результате взаимодействия проекций частиц возникает энтропийная сила, приложенная к геометрическому центру частицы. Следовательно, этот механизм может быть ответственным за появление массы. В результате кодирования информации на голографическом экране появляются масса / энергия, гравитация и само пространство-время. Необычный гироскоп можно использовать для детального изучения этого предположения.

Серия дальнодействующих сил, генерируемая в необычном гироскопе, позволяет нам контролировать гравитацию.

Устройство - необычный гироскоп может ответить на вопрос: действительно ли Голографический Принцип не гипотеза, а рабочая теория, согласно которому физика нашего трехмерного пространства-времени эквивалентна физике на двумерной гиперповерхности.

Таким образом, у нас есть простое уравнение движения для любой произвольно выбранной точки во Вселенной. Уравнение, которое на сертифицированном симуляторе демонстрирует динамику и множественные свойства частиц Стандартной Модели и место, где действительно существует наш трехмерный мир - это двумерный сферический ускоренно расширяющийся голографический экран (который обладает свойствами оптической голограммы, когда каждый пиксель голограммы несет информацию обо всех объектах). Работа необычного гироскопа описывается тем же уравнением. Это означает, что мы на правильном пути, экспериментальные данные подтверждают это.

Научная визуализация подтверждает необходимость срочного прототипирования модели необычного гироскопа. Подробности на моем сайте: www.isan.com.ua

Литература:
[1] J. M. Bardeen, B. Carter, and S. Hawking, “The four laws of black hole mechanics,” Commun.Math.Phys. 31 (1973) 161–170. https://projecteuclid.org/downl…/pdf_1/euclid.cmp/1103858973

[2] J. D. Bekenstein, “Black holes and entropy,” Phys.Rev. D7 (1973) 2333–2346.

[3] S. Hawking, “Black Holes and Thermodynamics,” Phys.Rev. D13 (1976) 191–197.

[4] L. Susskind, “The world as a hologram,” J.Math.Phys. 36 (1995) 6377–6396, arXiv:hep-th/9409089 [hep-th].
https://arxiv.org/abs/hep-th/9409089

[5] G. ’t Hooft, “Dimensional reduction in quantum gravity,” arXiv:gr-qc/9310026 [gr-qc].
https://arxiv.org/abs/gr-qc/9310026

[6] Erik Verlinde. "On the Origin of Gravity and the Laws of Newton". https://arxiv.org/pdf/1001.0785.pdf

[7] Margot M. Brouwer, Manus R. Visser, Andrej Dvornik, Henk Hoekstra, Konrad Kuijken, Edwin A. Valentijn, Maciej Bilicki, Chris Blake, Sarah Brough, Hugo Buddelmeijer, Thomas Erben,Catherine Heymans, Hendrik Hildebrandt, Benne W. Holwerda, Andrew M. Hopkins, Dominik Klaus, Jochen Liske, Jon Loveday, John McFarland, Reiko Nakajima, Cristóbal Sifón,Edward N. Taylor " "First test of Verlinde's theory of Emergent Gravity using Weak Gravitational Lensing measurements" https://arxiv.org/abs/1612.03034

[8] Niayesh Afshordi, Claudio Corian, Luigi Delle Rose, Elizabeth Gould, and Kostas Skenderis " Observational Tests of Holographic Cosmology" arxiv.org/pdf/1607.04878v2.pdf

[9] George F. Smoot "Cosmic microwave background radiation anisotropies: Their discovery and utilization" REVIEWS OF MODERN PHYSICS, VOLUME 79, OCTOBER–DECEMBER 2007.

[10] V. N. Samokhvalov “Non-electromagnetic Force Interaction in Presence of Rotating Mass in Vacuum,” [International Journal of Unconventional Science] 1(1), pp. 6-19, 2013 (Article received: 18 Nov 2012; Article accepted for publication: 23 Apr 2013) http://www.unconv-science.org/en/n1/samokhvalov/