Искусственные когерентные колебания материи

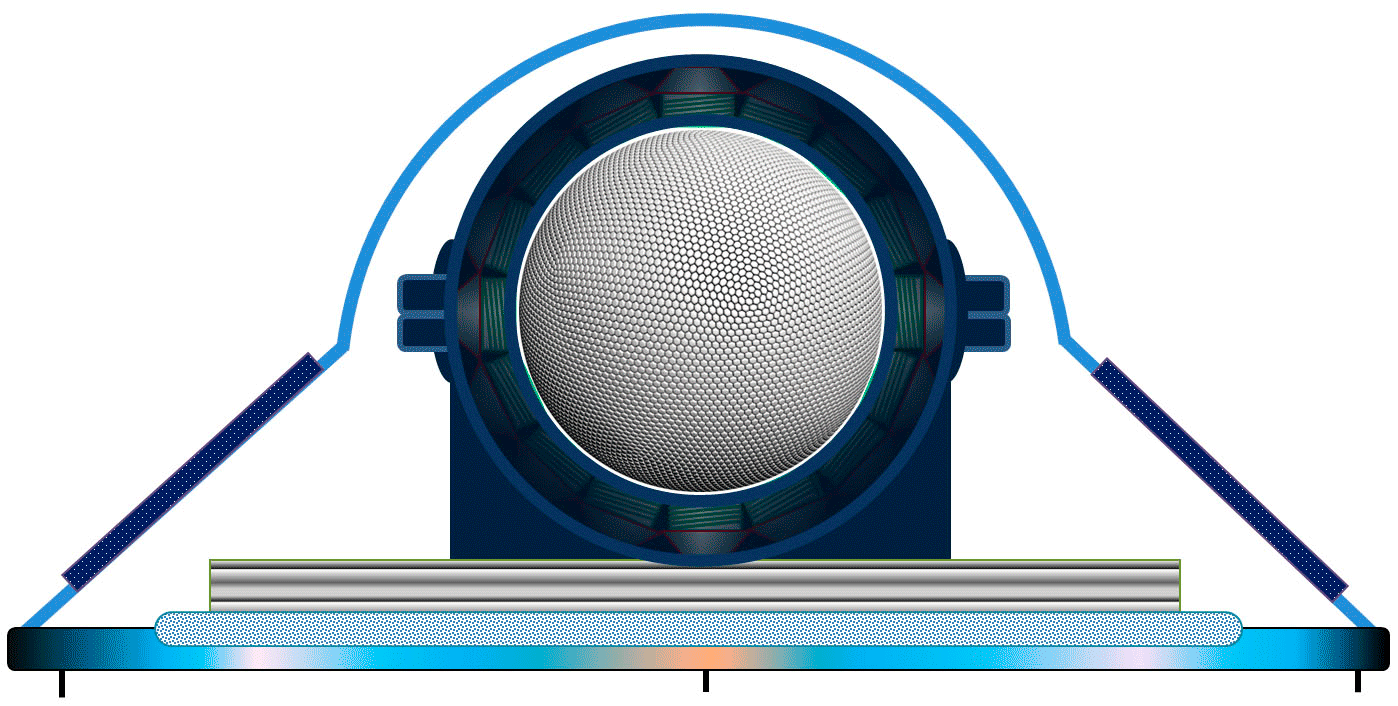
Всё началось с вопроса: можно ли создать когерентные колебания материи? Например, вращать сферический твёрдотельный ротор гироскопа определённым образом в вакуумированной полости статора вокруг трех осей за цикл, а не вокруг одной? И оказалось, что да, таки можно создать такое устройство - сферическую синхронную машину управляемую компьютером, у которой твёрдотельный ротор производит вынужденные когерентные колебания с постоянной разностью фаз от трёх искусственных источников.

Понятие когерентности сформировалось в начале XIX века после опытов английского ученого Томаса Юнга. В них две световые волны от разных источников падали на проекционный экран и складывались... .

Рассмотрим свет от двух обычных лампочек накаливания, которые дают некогерентное излучение на проекционный экран. Такой свет складывается просто: освещенность экрана равна сумме освещенностей от каждой лампы. У световых волн от лампочек разность фаз меняется по случайному закону с течением времени. Например, если в одну точку экрана сейчас пришли два максимума волны, то в следующий момент от одной лампы может прийти минимум, а от другой — максимум. Результат сложения волн даст «рябь на воде» — неустойчивую (подвижную), очень быстро меняющуюся интерференционную картину. Рябь световых волн столь быстра, что глаза не успевают за ней и видят равномерно освещенный экран. Если рассмотреть аналогию из мира звуков — это похоже на белый шум.

Однако, результат будет совсем другим, если на экране складываются две когерентные волны. В аналогии со звуком, если в звуковые каналы стерео акустической системы подать синусоидальные колебания от одного генератора и медленно менять относительные фазы колебаний в одном из каналов, то можно услышать как будет перемещаться мнимый источник звука из одной звуковой колонки в другую. Для света такие волны проще всего получить из одного лазерного пучка, расщепив его на две части, а потом их сложив. Тогда при сложении интенсивностей на экране возникнут полосы. Яркие — это области экрана, куда максимумы световых волн всегда приходят одновременно (в фазе). Замечательный оптический эффект состоит в том, что освещенность возрастет не в два раза, как в случае некогерентных волн, а в четыре. Это происходит потому, что в яркой полосе все время складываются максимумы волн, причём с постоянной разностью фаз, то есть их амплитуды, а освещенность пропорциональна квадрату суммы амплитуд волн. В тусклых полосах когерентные волны от разных источников гасят друг друга на экране.

Наша Вселенная устроена таким образом, что каждая частица вещества может проявлять свойства волны. Такие волны называют волнами материи, или волнами де Бройля. Замечательный французский физик Луи де Бройль в 1923 году предложил очень простую формулу, связывающую длину волны λ (расстояние между максимумами) с массой частицы m и ее скоростью v: λ = h/mv, где h — постоянная Планка.

Фундаментальное свойство волн любой природы — способность интерферировать. Однако чтобы в результате получить не равномерный шум, как и в случае со светом, яркую полосу, нужно обеспечить когерентность волн де Бройля. Этому мешает тепловое движение элементов массы, которые с разными скоростями различаются своими длинами волн. При охлаждении элементов массы, согласно формуле де Бройля, растет длина волны λ. И как только ее значение превысит расстояние между частицами, волны де Бройля разных частиц дадут устойчивую интерференционную картину, так как максимумы волн, отвечающие положению частиц, будут перекрываться.
Для того, чтобы создать когерентные колебания частиц (из которых состоит ротор необычного гироскопа) при более высоких температурах можно создать когерентные колебания самого сферического ротора. А проецировать на экран мы будем не свет, а невидимую интерференционную картину из ускорений элементов массы ротора.

Начнём с определения когерентного колебания ротора необычного гироскопа.

«Движение физического тела, при котором только одна его точка О остаётся всё время неподвижной, называется движением (вращением) твёрдого тела вокруг неподвижной точки О. В этом случае все точки физического тела движутся по поверхности концентрических сфер, центры которых находятся в точке О. Поэтому такое движение называют сферическим движением тела. Основываясь на определении сферического движения, получим параметрические уравнения вынужденного когерентного колебания элементов массы ротра.

«Когерентные колебания элементов массы — это сферическое движение физического тела, вынужденные полные гармонические колебания которого, последовательно выполняются триадами (поочерёдно за равные и короткие промежутки времени) угловыми перемещениями любых точек на пересечении осей, фиксированных декартовых координат с поверхностями концентрических сфер по законам косинуса и\или синуса».

θx = sin(θ),
θy = -sin(θ),
θz = cos(θ).

Где углы: θx — крен ; θy — тангаж ; θz- рысканье. Параметры θ= πt и -1 ≤ t ≤ 1; где θ — геометрический угол, отмеряемый, начиная с произвольного направления часовой стрелки, от соответствующей полуоси, а t задаёт необходимую точность угловых поворотов. Формула движения задана параметрически и применима для любого радиуса. Когда Δt → 0 и координаты центра масс ротора → 0 , мы имеем малый угол.

Малоугловое приближение является полезным упрощением основных тригонометрических функций, которое приближенно верно в пределе, когда угол стремится к нулю. Это усечения ряда Тейлора для основных тригонометрических функций в приближении второго порядка.

sin(θ)≅ θ

Согласно Голографическому Принципу: «В пределе очень большой области граничную поверхность можно считать плоской плоскостью на бесконечности». Тогда

sin(θ)= θ.

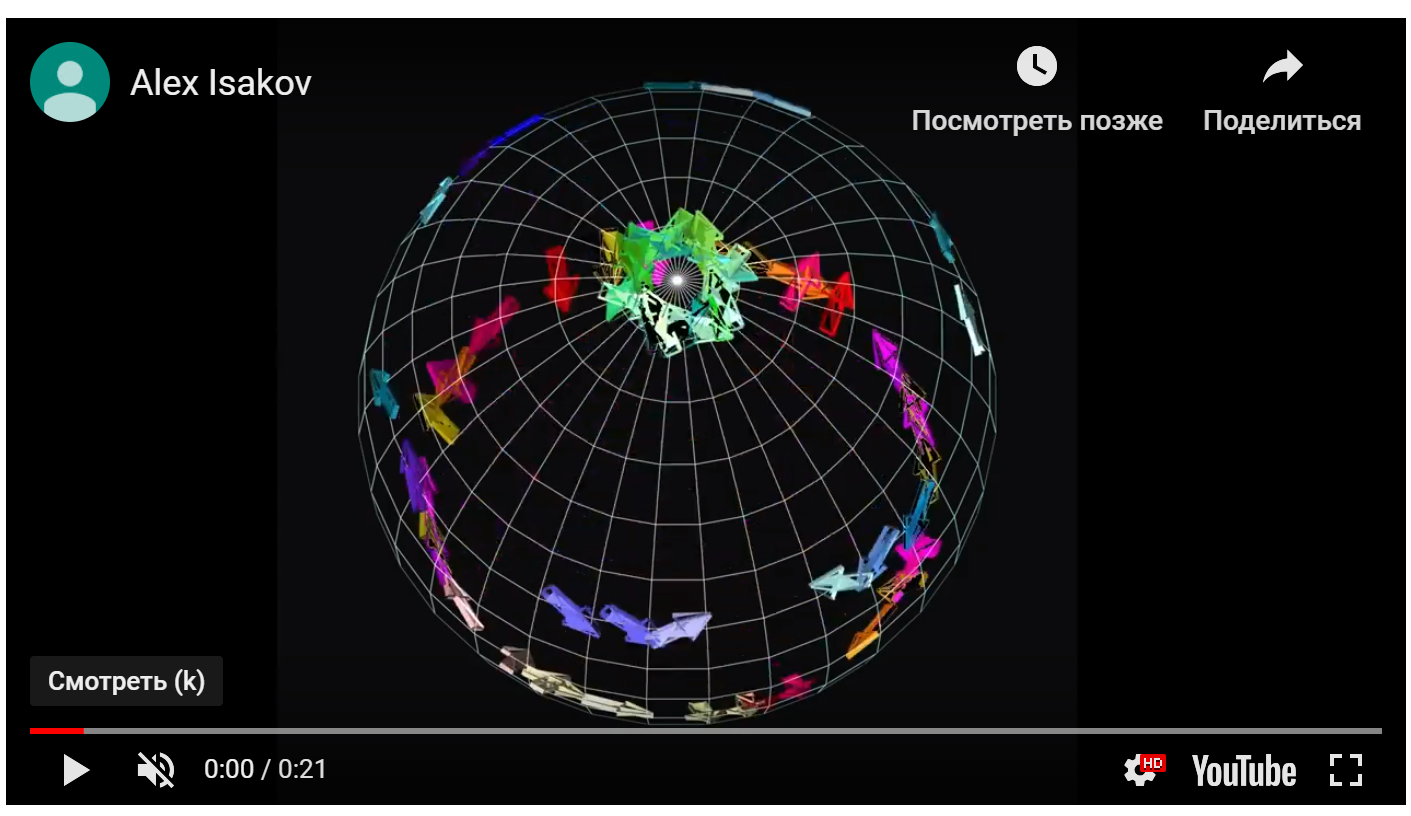
Эта формула когерентных колебаний элементов массы ротора необычного гироскопа просто показывает, как изолированная (идеализированная) классическая и одновременно квантовая система может вести себя в статистике с минимальным воздействием на систему. Если мы загрузим все 64 направления таких когерентных колебаний в компьютерный симулятор - программу для визуализации динамики в изометрии, мы сможем наблюдать свойства и, что очень важно, статистическую динамику всех элементарных частиц Стандартной Модели. На компьютерном симуляторе мы видим, как возникают две проекции каждой элементарной частицы как ведут себя центры проекций - элементарные частицы, как они обмениваются энергией, импульсом и взаимодействуют, и как они связаны друг с другом, чтобы сформировать более крупные структуры из трех поколений.

Мы можем видеть, что каждая «прыгающая» проекция каждой частицы, движущейся вдоль поверхности своей половины сферического голографического экрана, статистически связана со всей информацией о Вселенной, "живущей" на этом раздувающемся сферическом пузыре как градиенты температуры (условно непоказано).

Для элементов массы ротора необычного гироскопа, по аналогии с интерференцией света мы должны получить «яркую точку на экране» — малую область на поверхности, где максимумы от ускорений материи складываются в фазе. Неожиданно то, что когерентные волны многих и многих элементов массы могут занять одну область в пространстве, образуя как бы сверэлемент — набор огромного числа волн де Бройля. На языке квантовой механики это означает, что вероятность обнаружить когерентные элементы массы в «яркой точке» максимальна. Это удивительное состояние вещества называют конденсатом Бозе—Эйнштейна. Альберт Эйнштейн предсказал его в 1925 году на основании работ индийского физика Шатьендраната Бозе. В конденсате все элемнты массы находятся в одном квантовом состоянии и ведут себя как одна большая волна. Для элементов массы когерентно колеблющегося ротора необычного гироскопа скорость ротора шесть раз меняет направление, а, значит, первая производная от скорости - ускорение шесть раз обращается в нуль за равные промежутки времени цикла. Таким образом, мы имеем шесть одинаковых но диаметрально направленных групп ускорений которые можно без потерь проецировать "изнутри" и перемещать по голографическому экрану Вселенной без потерь. Но теперь, эту неподвижную интерференционную картину из шести групп ускорений элементов массы можно рассматривать в термодинамике не экране, поскольку, согласно Голографическому Принципу, ускорения прямо связаны с градиентами энтропии на экране.

ΔS ∼ α

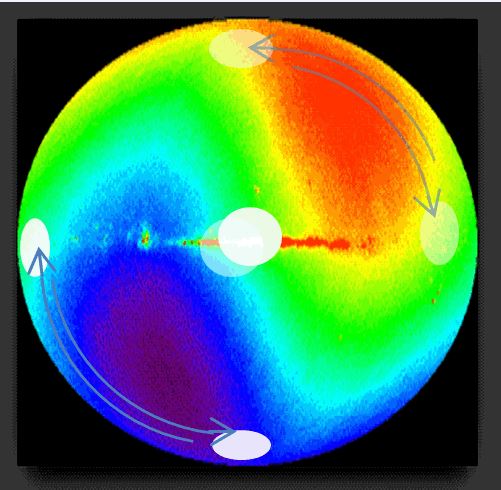
Проекции этих ускорений как белые круги показаны на фоне глобальной температурной анизотропии голографического экрана Вселенной.

Перемещая четыре из шести групп ускорений элементов массы ротора на фоне глобального градиента температуры на голографическом экране мы генерируем энтропийную (гравитационную) силу, действующую на расстоянии и приложенную к центру масс ротора.

F = ΔTΔS , это универсальный закон для всех сил и взаимодействий в нашей Вселенной. F — это универсальная энтропийная суперсила которая действует на её инфляционной голографической поверхности — 2D экране в результате перемещения информации/энтропии по ней.

Tермодинамические параметры: Fg — направленная гравитационная сила , ΔT— глобальный градиент температуры на голографическом горизонте Вселенной, ΔS — градиент энтропии, вызванный ускорением материи.

Fg = ΔTΔS.

Таким образом можно создавать серию гравитационных сил и управлять гравитацией, получить тандем компьютерного симулятора и необычного гироскопа - реального устройства для научной визуализации данных квантовых процессов - принципиально новый и недорогой инструмент для исследований в области квантовой физики и в космологии на уровне «яблок», работающий по единой формуле.

Подробности на моем сайте: www.isan.com.ua