Голографический Принцип как инженерная наука
Голографический Принцип
Сегодня Голографический Принцип - это сотни теоретических работ известных физиков мирового класса: Г. 'т Хоофта, Л. Сасскинда, Я. Д. Бекенштейна, Э. Верлинде, Х.М. Малдасены, Р. Буссо ... [1, 2, 3, 4, 5] . Уже есть экспериментальные исследования, подтверждающие работу Голографического Принципа [7,8] . С 1997 года опубликовано более 10 000 работ, поддерживающих эту идею.
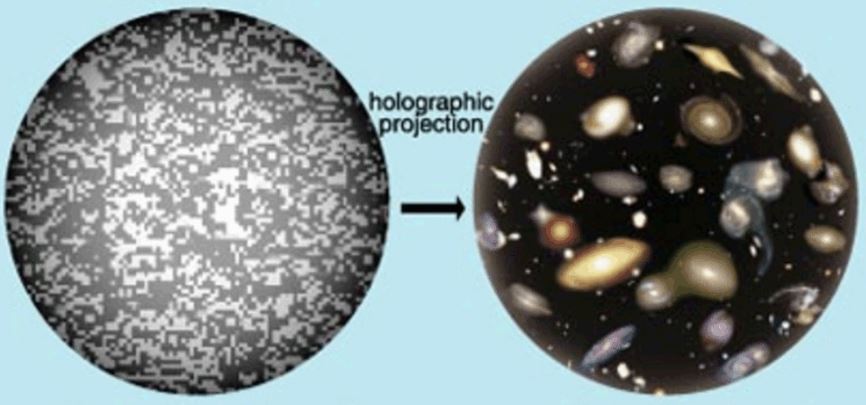
Одним из сюрпризов современной физики было открытие того, что мир является своего рода голографическим. Но еще более удивительным было то, что количество пикселей (бит), которые содержит эта голограмма, пропорционально площади поверхности, а не объёму. Другими словами: все, что есть, например, в вашей комнате, это голографическое изображение, записанное на двумерной поверхности стен, а если точнее, то на сферической поверхности экрана, окружающего эту комнату. То есть, на самом деле, в пределе, вы и вся остальная обстановка комнаты - всё это масштабная квантовая сферическая голограмма, записанная на поверхности, ограничивающая не только объем вашей комнаты, но и вообще, всю вселенную. В масштабах вселенной это сферическая и ускоренно инфляционная (раздувающаяся) поверхность или экран. Голограмма на инфляционном сферическом экране представляет собой двумерный массив крошечных пикселей, каждый из которых имеет размер порядка длины Планка. Конечно, природа квантовой голограммы и метод кодирования двухмерных данных сильно отличаются от технологии обычных оптических голограмм, но у них есть общие черты и свойства.
Например, изображение на экране вашего компьютера представляет собой двумерную поверхность заполненную светящимися пикселями. Каждый пиксель передает информацию об интенсивности и цвете плоского изображения. Но мы ограничимся только белым и чёрным цветом каждого пикселя. Как и изображение на фотографии, экран компьютера представляет собой плоский вид реальной трехмерной сцены. Однако, ваш мозг пытается воссоздать объём этой сцены, используя дополнительную информацию о светотени. Какой же способ кодирования информации необходим, чтобы надежно отображать информацию о трехмерном объекте, включая его внутреннее содержимое? Вместо набора пикселей, заполняющих плоскость, нам нужен набор пространственных элементов - вокселей, которые заполняют объем отображаемой сцены. Воксель представляет значение данных на регулярной сетке в трехмерном пространстве. Как и в пикселях в растровом изображении, сами вокселы обычно не имеют своей позиции жёстко связанной с координатами (адресами) носителя, в явном виде они закодированы вместе со своими значениями. Положение вокселя выведено на основании его положения относительно других вокселей (то есть его положение в структуре данных, составляющее одно объемное изображение). Заполнение пространства вокселями является гораздо более сложной задачей, чем заполнение поверхности пикселями. Например, если плоский экран компьютера имеет разрешение одной тысячи на тысячу пикселей, то для его заполнения вам понадобится миллион пикселей. Но если мы хотим заполнить объём, с тем же разрешением, то нам нужно 1000x1000x1000 = 1,000,000,000 миллиардов вокселов!
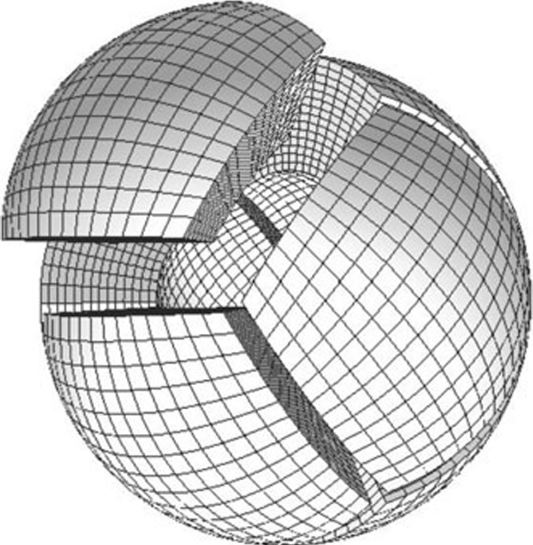
Однако естественный голографический метод записи информации на голографичеком экране вселенной сверх эффективен, что подтверждает предельно простая формула когерентных колебаний и возникновение (эмерджентность) из неё голографического экрана, а так же динамики и набора множества свойств всего зоопарка квантовых частиц Стандартной Модели, что будет продемонстрировано ниже. Голограмма вселенной представляет собой определённым и естественным образом составленные пикселы (биты информации на поверхности) которое позволяет однозначно восстановить полное трехмерное изображение используя только миллион пикселей, а не миллиард. Такая эффективность естественного кодирования информации на голографическом экране может быть изучена с помощью метода научной визуализации данных на моём сертифицированном программном симуляторе и измерена в квантовомеханическом устройстве – необычном гироскопе, работу которого мы рассмотрим ниже по тексту.
Оптическая голограмма является двумерным изображением и требует когерентных источников света для записи и воспроизведения (в случае с однослойными поверхностями), но содержит полную информацию о трехмерной сцене. Однако, если вы просто посмотрите на фотопластинку с изображением оптической голограммы, вы не увидите ничего значимого: изображение реального мира на плоской пластине искусственным образом закодировано. Для записи требуются два источника когерентных колебаний, а для воспроизведения требуется третий когерентный источник освещающий всю однослойную поверхность голограммы. Кодирование с помощью когерентных колебаний является общим свойством для всех видов однослойных голограмм как для оптических, так и для энтропийных. Отсюда возникает когерентность квантовой механики, которая подтверждает голографическую природу вселенной.
Информация на голографическом экране
Постулат. Мы отождествляем один бит информации с одной из фаз когерентных колебаний двух одномерных струн как фундаментальный бит естественного кодирования информации на одной площади Планка, принадлежащей замкнутой сферической и ускоренно расширяющейся поверхности голографического экрана. Одна площадь Планка - один бит информации, но уже две площади несут информацию из трёх бит, поскольку согласно термодинамике на голографическом экране. Энтропия измеряет микроскопическое количество информации, которая является невидимой для макроскопического наблюдателя. Когерентные колебания поверхности самого экрана не требуют дополнительного (третьего) источника когерентных колебаний. Результатом квантового измерения является выбор половины сферического экрана по которым перемещается пара безмассовых проекций имеющих разный спин. Забегая вперёд мы вначале постулируем, что перемещающаеся пара проекций квантовых частиц, каждая проекция по своей половине сферического голографического экрана, взаимодействуют с его глобальным градиентом температуры. Поэтому, в центре проекций возникает (эмерджент) элементарная частица.
Что даёт нам голографический формализм применённый к описанию вселенной?
У нас появляется возможность математически вывести фундаментальные законы физики, а не постулировать их после падения яблока, что уже продемонстрировано в работах Э Верлинде [6]. Полевая физика возникает (emerded) в результате голографического сценария и является его следствием. Поэтому эквивалентно, но совершенно по другому, без постулирования полей и экзотических частиц, раскрывается механизм возникновения (emerded) массы. Объясняются парадоксы квантовой механики, возникновение (emerded) гравитации и пространства - времени. С практической стороны мы получаем техническую возможность общаться с цивилизациями в нашей вселенной без ограничения расстоянием и скоростью света. Возникает возможность безреактивного перемещения в пространстве, искусственно управляя гравитацией без нарушения фундаментальных законов. Контролируемая гравитация позволит нам, в условиях приближённых к земным, испытывая постоянное искусственное ускорение 9,8G, эффективно путешествовать к планетам, к далёким звёздам и галактикам за разумное время и без необходимости использовать топливо. Известная ускоренная инфляция голографического экрана вселенной может быть использована для получения неисчерпаемой энергии и преобразование её в экологически чистую электрическую энергию. Но уже сегодня исследователям можно применить для изучения окружающего мира научный метод визуализации данных на компьютерном симуляторе в области квантовой физики, космологии, а завтра производить измерения принципиально новым способом, не прибегая к дорогостоящим ускорителям. И это далеко не полный список того, что кажется фантастикой и, что вполне практически реализуемый уже сегодня.
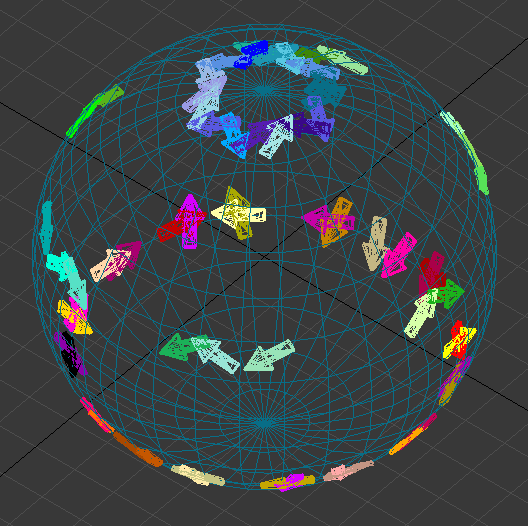
Фотография из видеодемонстрации динамики проекций частиц Стандартной Модели, выполненной на компьютерном симуляторе по предельно простой формуле когерентных колебаний.
Компьютерный симулятор как научный метод визуализации данных
Если мы загрузим уравнение движения точки в компьютерный симулятор (программу), мы увидим динамику этой точки. Для этого возьмем любую точку во Вселенной и произведем ее угловые перемещения вокруг одной оси Декартовых координат. После загрузки формулы на экране компьютера в изометрическом виде мы можем наблюдать обычный круговой поворот точки по кругу. Ничего примечательного. Но уже интересным способом происходит поворот выбранной нами точки вокруг двух осей. Симулятор демонстрирует характерную динамику точки на возникающей (эмерджентной) сфере и поворотные ускорения, которые направлениями связанны с неподвижными осями Декартовых координат. Но еще более удивительным является все возможные варианты угловых перемещений этой точки вокруг трех осей. Здесь подавляющее большинство экспертов будут выступать против такого заявления. Согласно теореме вращения Эйлера одновременное вращение вдоль ряда неподвижных осей в одно и то же время невозможно. Тем не менее, я обращаю ваше внимание, что для полного оборота точки или физического тела (ротора) вокруг трех фиксированных декартовых осей за цикл (цикл - это ключевое слово) вполне возможно. Симулятор демонстрирует это принципиально новое колебание точки и/или физического тела. В научной литературе описание таких колебаний отсутствует.
В это трудно поверить, но как только мы загружаем формулу угловых перемещений точки вокруг трех неподвижных осей, в соответствии с гармоническими законами, мы можем видеть возникновение (эмерджентность) сферического экрана и проекций всех элементарных частиц Стандартной Модели на нём!
На экране компьютера можно видеть 60 пар проекций частиц, динамику их трёх поколений, их спины и феномен «zitterbewegung» ... . Это, например, равносильно тому, что вы подключили к телевизору генератор случайных чисел, занесли в него начальную комбинацию двоичного кода, и в результате, на экране вы вдруг увидели, например, свой любимый фильм.
После запуска симулятора на сферическом экране, в изометрии, видны особые точки - полюса сферы и точки скопления, расхождения проекций частиц. Их можно идентифицировать как особые точки взаимодействия частиц и как узлы образования сложных составных частиц. Для составных частиц, часть проекций состоит из более сложных наборов их траекторий. Более сложные составные частицы, выражаясь физическим языком, имеют большее количество «намоток» проекций на поверхности сферы голографического экрана.
Каждому фундаментальному фермиону соответствует античастица с такой же массой. Все заряды антифермиона противоположны. Проекции античастиц, перемещающихся «назад по времени» тоже важны для исследования, но они пока исключены из рассмотрения в симуляторе.
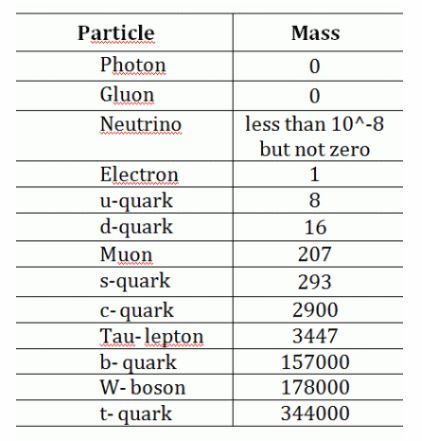
Поскольку множество проекций частиц в симуляторе отличаются положением и числом намоток на сферический голографический экран, то это может объяснить тот факт, что масса некоторых частиц может быть приблизительно выражена через массу электрона.
Если исследуемая нами точка принадлежит сферическому ротору гироскопа, то мы получаем необычный гироскоп. Вращение сферического ротора в вакууме вокруг трех декартовых осей за цикл имеет новые неизвестные свойства. Например, трёхмерные колебания ротора - когерентны и мы имеем неподвижную интерференционную картину из ускорений элементов массы ротора. Когерентность и интерференционный паттерн приводит нас голографии.
Если Голографический Принцип работает, то можно искусственно создать гравитационные силы дальнего действия, используя голографические свойства, например, кооперативные ускорения элементов массы ротора необычного гироскопа. Это устройство позволит нам контролировать гравитацию и иметь множество интересных приложений.
Необычный гироскоп

Необычный гироскоп - небольшое квантовомеханическое и электромехатронное устройство, работа которого описывается в области между классической и квантовой физикой. Эта область раньше считалась пустой. Однако, это устройство не больше ящика яблок. Сферический ротор необычного гироскопа имеет магниты и вращается в вакууме внутри сферического статора с индукторами под управлением компьютера (имеются датчики и драйверы для создания вынужденных колебаний ротора). Название необычный гироскоп оправдано тем фактом, что его ротор производит полные вынужденные колебания одновременно вокруг неподвижной точки – центра масс и трех фиксированных осей за цикл. Это предельно простое параметрическое уравнение угловых перемещений для точек ротора необычного гироскопа:
(θy= Sinθ,
(θz=-Sinθ,
где θx, θy, θz последовательные угловые смещения любой предварительно выбранной точки на поверхности ротора вокруг соответствующих осей неподвижных Декартовых координат (связанных с ускоренным наьлюдателем). Параметры: θ = πt и -1 ≤ t ≤ 1; θ - геометрический угол, определяемый произвольным и предварительно выбранным направлением угловых перемещений. Уравнение задается параметрически, и оно применимо для любого радиуса ротора. Мы можем задать максимальную точность угловых перемещений любой точки ротора, если Δt → 0 и имеем малоугловое приближение.
Малоугловое приближение является полезным упрощением основных тригонометрических функций, которое приближенно верно в пределе, когда угол стремится к нулю. Это усечения ряда Тейлора для основных тригонометрических функций в приближении второго порядка .
sin(θ)≅ θ
Согласно Голографическому принципу, в пределе очень большой области граничную поверхность - экран можно считать плоской плоскостью на бесконечности. Тогда проекции на голографический экран H = A = ∞, S — длина дуги — путь проектируемой точки и сегмент O-Line на голографическом экране. Следовательно, S = O и
sin(θ)= θ.
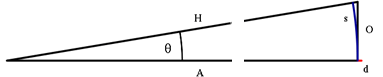
Свойства необычного гироскопа
Как только новый тип гироскопа был изобретен и тестировался на симуляторе, возник вопрос: какие новые свойства он может иметь?
Первое, что бросается в глаза, глядя на очень простое уравнение движения ротора, это то, что колебания ротора когерентны (обладают пространственной и временной когерентностью). Разность фаз таких колебаний является постоянной. Кроме того, используя симулятор, мы можем наблюдать фиксированную интерференционную картину из ускорений (α), направлениями связанных с полуосями фиксированных Декартовых координат. Мы видим шесть групп диаметрально расположенных ускорений точек ротора, которые мы можем сопоставить с его элементами массы. Если вычислить все возможные комбинаций направлений угловых перемещений точки по гармоническим законам, то их число будет ровно 60.
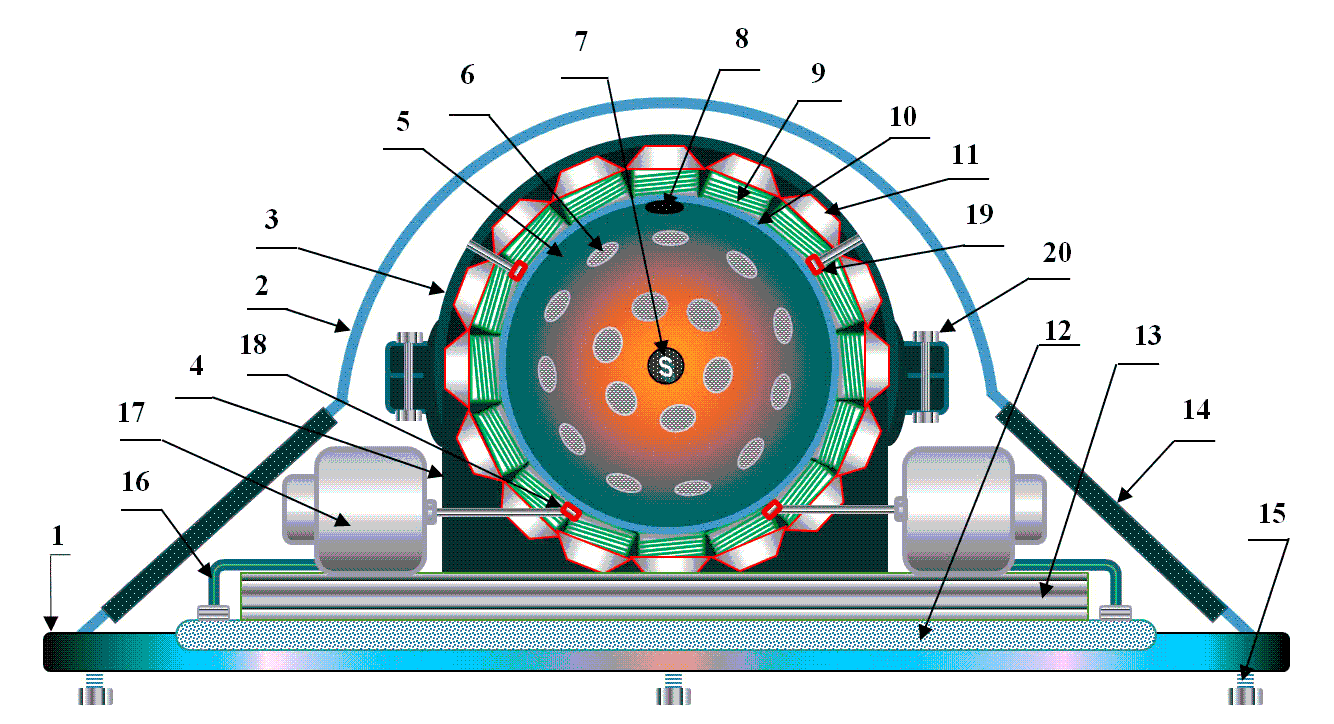
Эскиз конструкции:
- Основание.
- Оболочка.
- Статор (фронтальный разрез по диаметру).
- Стойка.
- Ротор.
- Магниты (66 шт.).
- Магнитная точка.
- Оптическая точка
- Катушки индуктивности (66 шт.).
- Датчики (магнитные и оптические).
- Ведомые микроконтроллеры и драйверы катушек индуктивности (микромодуль).
- Компьютер.
- Аккумуляторы.
- Солнечные батареи.
- Внешние крепёжные болты (4 шт.).
- Кабель.
- Вакуумный микронасос (4 шт.).
- Цифровой вакууметр и электромагнитный клапан (4 шт.).
- Цифровой инфракрасный датчик температуры и предохранительный термоклапан (4 шт.).
- Крепёжные болты для полусфер статора (16 шт.)
Необычный гироскоп это принципиально новый тип гироскопа, который отличается от любых силовых гироскопов не только отсутствием механических осей и отсутствием газовой подушки, но и когерентными колебаниями сферического ротора в вакуумной полости статора. В то время как ротор традиционно приводимого в действие силового гироскопа совершает полное вращение вокруг одной и той же оси за один цикл, ротор необычного гироскопа вынужден быстро вращаться вокруг трех осей (Ox, Oy, Oz). Это его концептуальное отличие от любого гироскопа, и эта особенность отражена автором этого текста в формуле патентной заявки. Левитация ротора внутри статора достигается путем его активной электромагнитной подвеске под управлением компьютерной системы. Как правило, в трехосных гироскопах используется карданный подвес, который позволяет свободно вращать ротор относительно трех осей, и именно это делает их несколько похожими на необычный гироскоп. Но только похожими. Вынужденные и полные колебания ротора необычного гироскопа вокруг трех осей за цикл - это его принципиальное отличие от любого силового гироскопа.
Таким образом, за цикл когерентных колебаний ротор необычного гироскопа совершает один полный оборот вокруг одной неподвижной точки - это геометрический центр, центр масс и центр ускорений ротора и одновременно вокруг трех осей декартовых координат.
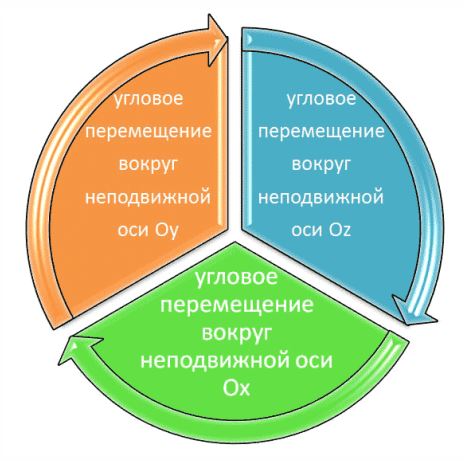
Например, нам дана точность угловых перемещений ранее выбранной нами точки на роторе: Δt = 1/360. Это означает, что мы начали делать угловые перемещения этой точки, в постоянном и минимальном временном интервале, на поверхности ротора примерно на один градус, например, согласно закону (Cosθ) и вокруг фиксированной оси x. В следующем равном и минимальном временном интервале мы можем производить угловые перемещения этой точки вокруг оси y, но уже по закону (Sinθ) и соответственно для z (- Sinθ). Но поскольку для каждой оси до конца цикла осталось около 359 градусов, то мы продолжим такими триадами последовательно производить угловые перемещения точки, которые в конечном итоге будут заканчиваться одновременно для всех функций, так как разность их фаз постоянна. Мы получили цикл когерентных колебаний. Нам пока еще не нужно знать, как ведут себя точки ротора, каковы их траектории. Функции чередуются и есть шесть групп направленных (мгновенных) вращательных ускорений, связанных с фиксированными декартовыми координатами. В пространстве и во времени цикла они занимают постоянные позиции. Таким образом, нами получены когерентные колебания всех точек ротора необычного гироскопа в вакууме и силы Кориолиса, действующих на каждый его элемент массы.
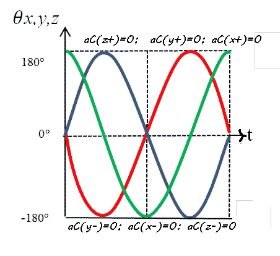
Принцип эквивалентности говорит нам о том, что мы не можем отличить инерционную и гравитационную массу от эксперимента. Эйнштейн изобрел эксперимент с лифтом. Лифт бесконечно удален от гравитирующих тел в пространстве и движется с ускорением. Тогда все тела в лифте будут находиться под действием инерции и окажут давление на пол лифта. То есть тела будут иметь вес. Если лифт не движется, а висит над гравитирующей массой в однородном поле, все тела также окажут давление на пол в лифте. Таким образом, почти невозможно различать эти две силы. Поэтому все механические явления будут происходить практически одинаково в обоих лифтах. Эйнштейн распространил это утверждение на все массы физических тел во Вселенной. Если мы ищем способ контролировать гравитацию, и аксиома Эйнштейна позволяет нам не различать силы инерции и силы тяжести, мы должны воспользоваться этой возможностью и на практике использовать силы инерции, которые зависят от скорости. Например, это сила Кориолиса, которая отклоняет тело от прямолинейного движения, если эти тела находятся во вращающейся неинерциальной системе отсчета.
Сила Кориолиса
Величина сил Кориолиса зависит от угловой скорости ротора. Можно предположить, что суперпозиция сил Кориолиса, полученная таким образом, эквивалентна фиктивному «гравитационному» полю, действующему на каждый элемент массы ротора. Поскольку все силы Кориолиса равны друг другу и ортогональны, их сумма будет равна нулю и, значит, центр масс ротора останется неподвижным. Но мы можем увеличить эти силы Кориолиса за счет увеличения скорости когерентных колебаний ротора.
Кроме того, у нас есть возможность одновременно смещать все точки (все элементы массы), например, вокруг любых двух из трех фиксированных осей Декартовых координат, искусственно, и за короткое время, разрушая когерентные колебания, при этом создавая кратковременную декогеренцию. Мы можем технически сделать это в конце каждого цикла, используя компьютерную систему управления движением ротора. В то же время мы не нарушаем Третий Закон Ньютона, пока не утверждаем, что центр массы ротора должен изменить свое положение в пространстве в такой замкнутой системе. Центр масс ротора должен остаться в полном покое при полном равенстве сил Кориолиса действующих на него, как при когерентных колебаниях ротора, так и в момент искусственно производимой декогеренции. Направленная гравитационная сила, согласно Закону Сохранения Импульса, не должна возникать.
Но совсем другое дело, если работает Голографический Принцип и его Закон Сохранения Информации, что косвенно подтверждается в экспериментах. На самом деле мы имеем дело с единственной фундаментальной теорией, которая позволяет нам расширить размер закрытой системы до ее максимального размера - голографического экрана вселенной.
Закон Сохранения Информации и глобальная температурная анизотропия вселенной.
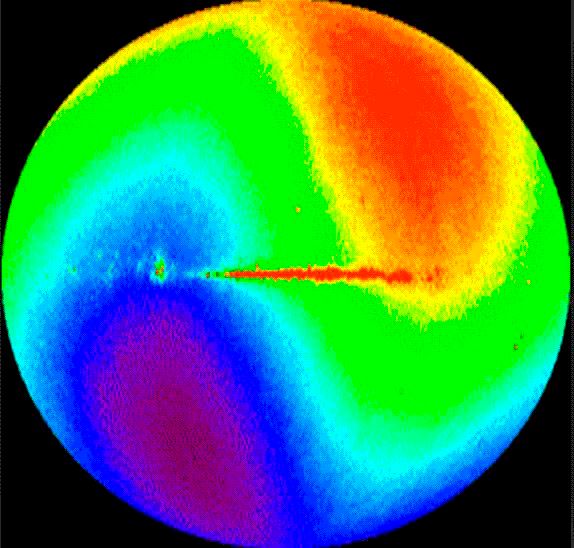
Для получения направленной гравитационной силы в необычном гироскопе нам необходимо воспользоваться глоальным градиентом температуры голографической поверхности и использовать законы термодинамики.
До возникновения Голографического Принципа соизмеримое с ним по масштабности, было обнаружение анизотропии Вселенной, известной как анизотропия космического микроволнового фона реликтового излучения РИ. По сути это крупномасштабная разница температуры в разных направлениях на небе [9]. Экспериментально подтверждённая дипольная анизотропия вселенной и открытие когерентных акустических волн, имеет большое значение не только для космологии, но и для всего естествознания в целом. Когерентность колебаний в ранней вселенной так же подтверждает голографическую природу вселенной. Можно сказать, что крупномасштабные трехмерные звуковые когерентные колебания в ранней вселенной действовали до периода рекомбинации и закончились через 379 000 лет после Большого Взрыва. Однако звуковые когерентные колебания не исчезли, а зафиксировали большой масштаб глобального градиента температуры на голографическом экране. Поэтому сегодня мы можем наблюдать глобальный градиент температуры вселенной, фотографируя её со спутников в космосе.
Согласно Голографическому Принципу, мы можем производить проекцию РИ и проекцию градиентов энтропии, отражающей перемещение материи на голографический экран, без потери информации. Зафиксированный спутниками масштабный глобальный градиент температуры на голографическом экране – фундаментальный элемент, который взаимодействует с перемещающимися проекциями. Например, исследуя динамику проекций квантовых частиц на симуляторе, этот механизм взаимодействия глобального градиента температуры демонстрирует возникновение (эмерджентность) массы у частиц, указывает на точное число элементарных частиц и число частиц, не обладающих массой (60 и 4, соответственно).
Для того, чтобы исследовать термодинамику на голографическом экране, мы должны учитывать влияние проекций РИ на динамику проекций ускорений элементов массы, перемещающихся по экрану. Рассматривая результаты работы симулятора, динамику проекций частиц мы учитываем эту разницу в температуре сферического экрана. Отсюда можно предположить, что Голографический Принцип может выявить новый голографический механизм генерации масс частиц и всех известных сил и взаимодействий. В качестве единой силы может выступить энтропийная сила, действующая на голографическом экране.
Контроль гравитации на основе необычного гироскопа.
Итак, примерно половина глобальных градиентов температуры на голографическом экране Вселенной отличается друг от друга, поэтому две из четырех групп градиентов энтропии (белые круги на фотографии) из-за движения элементов массы ротора при смещении, в момент искусственно произведенной декогеренции, испытывают разное по величине взаимодействие с этими областями. Крупномасштабное нарушение симметрии на голографическом экране и результат декогернции колебаний элементов массы ротора приводят к направленной энтропийной силе, приложенной к центру масс ротора необычного гироскопа.
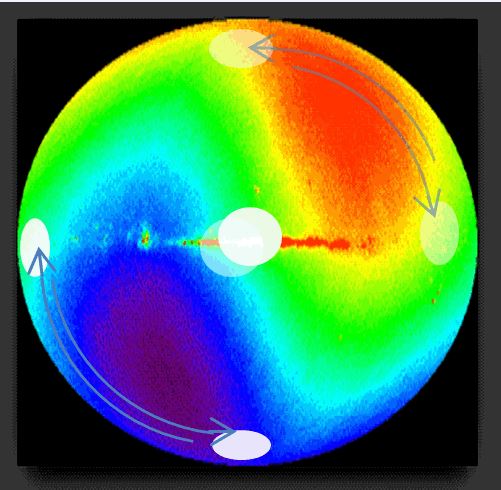
Согласно голографическому принципу изменение этой энтропии при перемещении вещества приводит к энтропийной силе, которая принимает вид гравитационной силы.
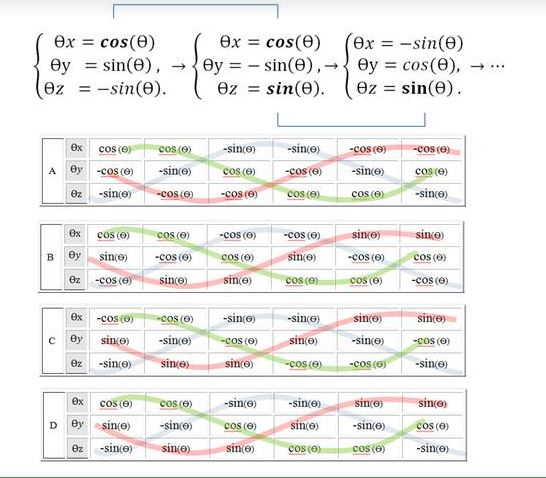
В таблицах демонстрируется варианты декогеренции колебаний в разных направлениях, в результате которых происходят смещения и возникает дальнодействующая гравитационная сила.
Fg = ΔTΔS,
где Fg гравитационная сила,
ΔT – глобальный градиент температуры на космологическом горизонте,
ΔS - энтропийный градиент, возникающий в результате перемещения вещества
(смещений на голографическом экране проекций ускорений элементов массы ротора), ΔS ~ α.
После преобразований мы приходим ко второму закону Ньютона [6], а это означает, что гравитационную силу можно искусственно получать без экзотических масс и энергий, что приводит нас к контролю над гравитацией.
Таким образом, интегральный гравитационный эффект определяется множеством энтропийных сил, взаимодействующих с крупномасштабной (глобальной) дипольной анизотропией, представленной температурой на голографическом экране Вселенной. Гравитация - это термодинамическое явление. Ряд сгенерированных управляемых и направленных сил гравитации позволяет нам осуществлять смещение всей конструкции необычного гироскопа в пространстве в любом выбранном направлении нереактивным способом. Это означает, что для одной точки - центра и для всех точек, т. Е. Центра масс ротора необычного гироскопа, гравитация, например, гравитация Земли, может быть полностью компенсирована и / или преодолена. Сегодня многочисленные эксперименты с быстрым вращением массы в вакууме (7000 об/мин) демонстрируют силы, действующие на расстоянии, величиной в 2,5 Н. Идея о том, что гравитационная сила может рассматриваться как действующая на расстоянии энтропийная сила, подтверждается в независимом эксперименте [10].
Выводы.
Если мы рассмотрим все возможных направления когерентных колебаний ротора необычного гироскопа, то их число будет ровно 60. Это число соответствует числу элементарных частиц Стандартной Модели. И действительно, после загрузки в сертифицированный симулятор чрезвычайно простой формулы, описывающей динамику ротора необычного гироскопа, на экране компьютера в изометрии можно наблюдать появление сферического экрана, а также динамику и свойства элементарных частиц. Принцип голографии заключает, что: гравитация объясняется как энтропийная сила. Принцип эквивалентности приводит нас к выводу, что на самом деле это закон инерции, происхождение которого энтропическое. Эта термодинамика на экране, возникающая из-за статистического поведения микроскопических степеней свободы локализованных на голографическом экране Вселенной. Таким образом, сила тяжести и его дальность не постулируются, а производятся из голографического сценария, и представляет собой результат естественной или искусственной декогеренции квантовых процессов. Этот же механизм, но без декогеренции ответственен за появление массы у частиц. Результатом кодирования информации на голографическом экране становится масса / энергия, гравитация и пространство-время. Необычный гироскоп можно использовать для детального изучения этого предположения. Ряд, созданных и направленных дальнодействующих гравитационных сил, позволяет нам контролировать гравитацию. Устройство, также, может ответить на вопрос: действителен ли Голографический Принцип, согласно которому физика нашего трехмерного пространства-времени эквивалентна физике на двумерной поверхности. У нас есть простое уравнение движения для любой произвольно взятой точки во Вселенной. Уравнение, которое на сертифицированном симуляторе демонстрирует многие свойства частиц Стандартной Модели и само место, где действительно существует наш трехмерный мир - сферический голографический экран вселенной.
Работа необычного гироскопа описывается тем же уравнением, которое мы закладываем в компьютерный симулятор. Таким образом мы доказываем корреляцию информации на квантовом уровне, на уровне яблок и в космологических масштабах. Это означает, что мы на правильном пути и экспериментальные данные подтверждают это. Научная визуализация данных говорит нам о необходимости срочного прототипирования модели необычного гироскопа. Детали на моём сайте: https://www.isan.com.ua
Литература
[1] J. M. Bardeen, B. Carter, and S. Hawking, “The four laws of black hole mechanics,” Commun.Math.Phys. 31 (1973) 161–170.
[2] J. D. Bekenstein, “Black holes and entropy,” Phys.Rev. D7 (1973) 2333–2346.
[3] S. Hawking, “Black Holes and Thermodynamics,” Phys.Rev. D13 (1976) 191–197.
[4] L. Susskind, “The world as a hologram,” J.Math.Phys. 36 (1995) 6377–6396, arXiv:hep-th/9409089 [hep-th].
[5] G. ’t Hooft, “Dimensional reduction in quantum gravity,” arXiv:gr-qc/9310026 [gr-qc].
[6] [Verlinde, 2010] Erik Verlinde. "On the Origin of Gravity and the Laws of Newton". http://arXiv:1001.0785v1 [hep-th].
[7] Margot M. Brouwer, Manus R. Visser, Andrej Dvornik, Henk Hoekstra, Konrad Kuijken, Edwin A. Valentijn, Maciej Bilicki, Chris Blake, Sarah Brough, Hugo Buddelmeijer, Thomas Erben,Catherine Heymans, Hendrik Hildebrandt, Benne W. Holwerda, Andrew M. Hopkins, Dominik Klaus, Jochen Liske, Jon Loveday, John McFarland, Reiko Nakajima, Cristóbal Sifón,Edward N. Taylor " "First test of Verlinde's theory of Emergent Gravity using Weak Gravitational Lensing measurements"https://arxiv.org/abs/1612.03034
[8] Niayesh Afshordi, Claudio Corian, Luigi Delle Rose, Elizabeth Gould, and Kostas Skenderis " Observational Tests of Holographic Cosmology"arxiv.org/pdf/1607.04878v2.pdf
[9] George F. Smoot "Cosmic microwave background radiation anisotropies: Their discovery and utilization" REVIEWS OF MODERN PHYSICS, VOLUME 79, OCTOBER–DECEMBER 2007.
[10] V. N. Samokhvalov “Non-electromagnetic Force Interaction in Presence of Rotating Mass in Vacuum,” [International Journal of Unconventional Science] 1(1), pp. 6-19, 2013 (Article received: 18 Nov 2012; Article accepted for publication: 23 Apr 2013) http://www.unconv-science.org/en/n1/samokhvalov/