Академия: Введение в функциональное программирование. Конспект пятой недели курса
Привет. Я участвую в проекте Академия от @ontofractal и продолжаю знакомить вас с конспектами курса Введение в функциональное программирование от Delft University of Technology. Сегодня мы познакомимся с мощным инструментом, позволяющим генерировать сложные структуры данных с помощью набора простых правил - генераторами списков. Но прежде чем перейти к этой теме, я хотел бы сказать пару слов о том, почему мы так часто обращаемся к спискам, и какое место они занимают в ФП-инструментарии

Почему списки?
Об этом мало кто задумывается, но вообще списки - это одна из старейших структур данных из существующих поныне. Их история берет начало с середины 50-х годов, когда в рамках проекта The General Problem Solver был создан язык, названный IPL - Information Processing Language. Целью этого проекта было создание компьютерной программы, способной решить любую существующую проблему, при условии наличия подъодящего описания. Предполагалось, что программа будет получать вопрос, построенный при помощи некоторых логических операций, таких как дизъюнкт Хорна, и путем определенных вычислений давать на него ответ. И хотя эта амбициозная задача, конечно, не была решена, разработка этой системы оказало большое влияние на развитие компьютерных наук. В частности, именно в IPL были впервые реализованы такие привычные для нас понятия, как функции высшего порядка, а также списки и операции над ними
Следующей вехой в развитии программирования стало создание Лиспа, который появился на свет спустя пару лет после IPL. Списки стали одной из фундаментальных структур данных в этом языке, и, собственно, название этого языка является акронимом к фразе Lots of Irritating Single Parentheses List Processing. Более того, сам код программы, написанной на Лиспе - это по сути, простой список, и работу интерпретатора можно в упрощенном виде представить как перебор элементов этого списка. Подобный подход к построению конструкции программ сделал написание интерпретаторов довольно простым процессом
Подобная спискоцентричная структура оказалось с одной стороны простой для понимания, а с другой - обладала огромной выразительно мощью, поэтому с момента возникновения Лиспа была разработана огромное количество диалектов, некоторые из которых (например, Common Lisp или Clojure) популярны по сей день
Так почему же списки стали столь популярной структурой данных в среде поклонников ФП? Думаю, причин здесь несколько. Во-первых, списки - это очень абстрактный и, следовательно, простой в использовании вид данных. Так, например, для работы со словарями нам нужно знать их ключи, для стеков важен порядок добавления элементов, в то время как для списков не требуется практически ничего, и даже порядок элементов зачастую не играет особой роли при использовании функциональных техник. Большая часть работы со списками в ФП осуществляется при помощи абстрактных процедур, вроде map, filter, fold, zip etc
Во-вторых, списки - это рекурсивная структура данных. В предыдущих частях мы уже отмечали, что каждый список состоит из двух элементов: начала и остатка, а остаток в свою очередь тоже делится на начало и остаток, и так далее, пока остаток не станет пустым списком (к слову, такую схему организации списков Хаскель позаимствовал у Scheme, одного из диалектов Лиспа). А так как рекурсия - это единственный способ организовать циклические действия в функциональных языках, то было бы логичным использовать наиболее подходящую для подобных функций структуру данных

Преимущества и недостатки списков
Генераторы списков
Теперь, когда мы поняли, чем же так хороши списки, пришло время перейти к основной теме сегодняшней части
Генераторы списков - это механизм, попавший в Хаскель из математики, или, если быть точнее, из теории множеств. Множество - это просто набор элементов. Самый простой способ его задать - это перечислить все элементы в фигурных скобках: {1, 2, 3, 4}. Однако, зачастую требуются более сложные множества, элементы которого подобраны на основе какого-либо правила. Как раз для таких случаев существуют нотация с использованием условий (set builder notation), которае выглядят следующим образом: {x | x > 7}. Эта запись обозначает множество всех вещественных чисел больше 7. Подобным образом работают и генераторы списков в Хаскеле
Разобравшись с теорией, я предлагаю запустить GHCi и перейти к практике. Для начала попробуем создать список квадратов чисел от одного до десяти:
Prelude> [x^2 | x <- [1..10]]
Такая запись даст нам следующий результат:
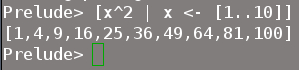
Отлично. Теперь разберемся, как это работает. Часть выражения, расположенная справа от вертикальной черты, создает исходный список, извлекает поочередно элементы из него и связывает с переменной х. Левая часть описывает действия, которые нужно произвести над этой переменной.
Что еще более интересно, генераторов может быть несколько. Например, выражение
> [(x,y) | x <- [1..3], y <- [1..3]]
Даст нам следующий список:

Так, кажется, здесь все несколько сложнее, чем в первом случае. Давайте разбираться. Первая группа элементов - это кортежи, в которых х = 1, а у варьируется от 1 до 3. Вторая группа - это кортежи, в которых х = 2 комбинируется с у = 1 .. 3, и, наконец, третья группа - это кортежи с х = 3 и у = 1 .. 3. Похоже, что второй генератор является вложенным по отношению к первым. Для упрощения понимания приведу пример из императивного языка:
def main(): generatedList = [] for x in range(1, 4): for y in range(1, 4): tupl = (x, y) generatedList.append(tupl) print(generatedList)main()который даст аналогичный результат:

Disclaimer: этот код приведен в обучающих целях, и на самом деле нет смысла создавать списки таким путем, потому как в Питоне начиная с версии 2.0 тоже есть генераторы списков:
Fahrenheit = [ ((float(9)/5)*x + 32) for x in Celsius ]
И, к слову, этот пример подтверждает тезис, что техники, которые мы изучаем, могут пригодиться не только при программировании на Хаскеле
Теперь давайте перейдем к более полезным примерам и напишем функцию, "уплощающую" списки, состоящие из вложенных списков. Если бы мы отказались от использования функциональных техник и опирались на решения вроде for, нам бы пришлось иметь дело с многострочными конструкциями, вроде приведенной выше. С использованием генераторов та же задача решается в одну строку:
concat :: [[a]] -> [a]concat xss = [x | xs <- xss, x <- xs]Фильтры
Выше я упоминал, что генераторы множеств могут создавать элементы на основе определенных условий (например, х > 7). Подобные фильтры есть и у генераторов списков. Например, представим, что нам нужно получить все четные числа от одного до ста. Это легко осуществить, просто выставив в качестве фильтра функцию even, возвращающую True или False в зависимости от того, четное ли число:
[x | x <- [1..100], even x]

Вуаля!
Комбинируя генераторы с соответствующими фильтрами, порою можно добиться воистину удивительных результатов. Например, если вы помните, в известном фильме "Куб" героям постоянно приходилось решать головоломки, связанные с поиском простых чисел, и в итоге немалая часть экранного времени уходит на вычислительную муть. Но все было бы куда веселее, будь у героев под рукой компьютер с GHCi, ведь тогда они могли бы решить свою задачу, просто написав правильный генератор списков:
factors :: Int -> [Int]factors n = [x | x <- [1..n], n `mod` x == 0]prime :: Int -> Boolprime n = factors n == [1, n]primes :: Int -> [Int]primes n = [x | x <- [2..n], prime x]На выходе мы получил сколь угодно длинный список простых чисел, и все что нам в итоге будет нужно - проверить, есть ли наше число в этом списке

Общая структура генераторов списков
Что показалось самым интересным на этой неделе
В этой части мы познакомились с очень интересной техникой, позволяющей "на лету" генерировать довольно сложные списки. Более того, генераторы списков обладают очень простым синтаксисом, позволяющим осуществлять задуманное в одну строчку кода, в то время как императивные техники, вроде циклов for, требуют куда больше усилий
Анонс следующей части
В следующей части мы закончим со списками и начнем изучать рекурсивные функции. Обычно люди, не знакомые с ФП, считают эту тему сложной и думают, что повторяющиеся действия гораздо проще создавать при помощи циклом for или while. Я надеюсь, мне удастся развенчать этот миф, и показать, что рекурсия - это очень простое и в то же время выразительное средство, позволяющее писать более понятный и лаконичный код